Les comparaisons sont ici présentées avec des fonctions, mais sont aussi valables pour les suites.

Fonction négligeable

On dit que \(f\) est négligeable en \(a\) devant \(g\) si :
\[ \displaystyle \lim_{x \to a} \frac{f(x)}{g(x)} = 0 \]
On écrit alors
\[ f = o_a(g) \quad ou \quad f \ll_a g \]
La relation de négligeabilité est transitive, et stable par combinaison linéaire ainsi que par produit.
Quelques exemple de fonctions négligeables :

• \(x^a = o_0(x^b) \Leftrightarrow a > b\)
• \(x^a = o_{+ \infty}(x^b) \Leftrightarrow a < b\)
• \(ln^a(x) = o_{+ \infty}(x^b)\)
• \(x^b = o_{+ \infty}(e^{cx})\)

Fonction dominée

On dit que \(f\) est dominée par \(g\) si:
\[ \exists \epsilon, \forall x \in \overline a, \mid\frac{f}{g}\mid < \epsilon \]
On le note \(f = O_a(g)\). Cette notation est très utilisé en informatique pour représenter la complexité des algorithmes.
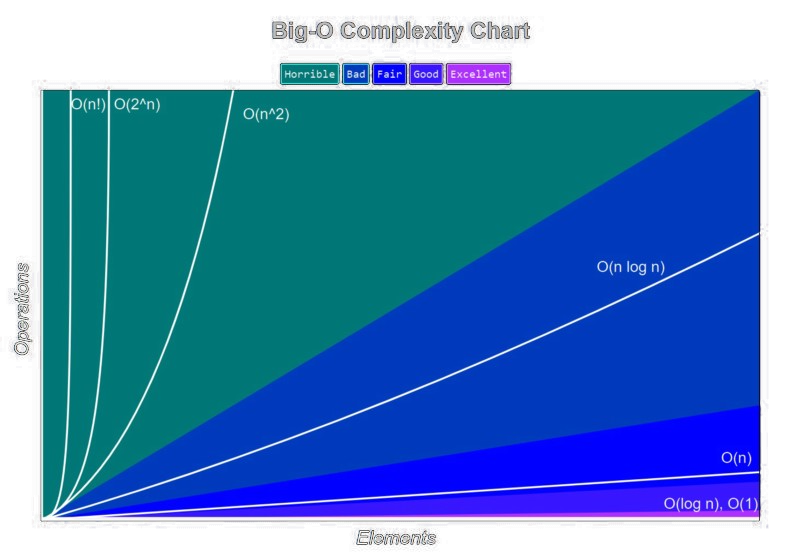
De meme que les fonctions négligeables, la domination est stable par combinaison linéaire et par produit. De plus elle est transitive.

Equivalence

On dit que les fonctions \(f\) et \(g\) sont équivalentes si
\[ \displaystyle \lim_{x \to a} \frac{f(x)}{g(x)} = 1 \]
On écrit alors \(\displaystyle f \sim_a g\). De la on obtient que \(f-g \ll g\).
Comme son nom l'indique, \(\sim\) est une relation d'équivalence, stable par produit et par quotient. L'équivalence est stable par composition a droite.

Echelle des infiniment grands

\[ 1 \ll ln(ln(n)) \ll ln^a(n) \ll n^a \ll a^n \ll n! \ll n^n \]